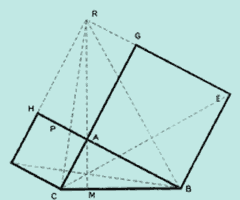
Доказательство предложено Ренаном в 1889 году. Треугольники HRA и ABC равны, поэтому равны отрезки RA и BC. Заметим, что треугольник IBC равен треугольнику CAK, а треугольник FBC равен треугольнику BAR. Легко доказать, что отрезки KA и BC, BI CR, CF и BR взаимно перпендикулярны. Т.к. RA (RM), BI и CF являются высотами треугольника BCR и поэтому пересекаются в одной точке, площадь треугольника CAR есть 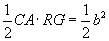, а площадь треугольника BAR есть 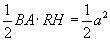. Следовательно, сумма площадей треугольников CAR и BAR есть 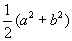. Но площадь треугольника CAR есть 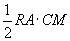, а площадь BAR есть 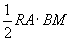, следовательно, сумма площадей треугольников CAR и BAR есть, т.е.. 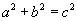Теорема доказана.