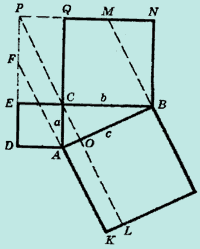
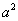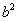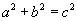Рисунок иллюстрирует доказательство, приведенное Нассир-эд-Дином (1594 г.). Здесь: PCL - прямая; равновеликие четырехугольники KLOA, ACPF, ACED имеют площадь ; равновеликие четырехугольники LGBO, СВМР, CBNQ имеют площадь ; кроме того, площадь четырехугольника AKGB равна сумме площадей четырехугольников AKLO и LGBO и равна ; отсюда . Теорема доказана.