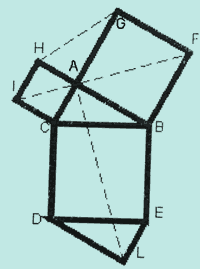
Доказательство предложено Темпельгофом в 1769 году. На рисунке треугольники LDE и ABC равны; треугольники AGH и ABC равны; четырехугольники LDCA, FBCI и ABEL являются равновеликими, кроме того, равновелики IHGF и ICBF, следовательно, равновелики шестиугольники ICBFGH и ACDLEB. Эти шестиугольники имеют общий треугольник ABC, а также равные треугольники AGH и LDE, и следовательно остальные части этих многоугольников являются равновеликими, а это значит, что площадь четырехугольника CDEB равна сумме площадей четырехугольников CAHI и ABFG, т.е. 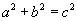. Теорема доказана.