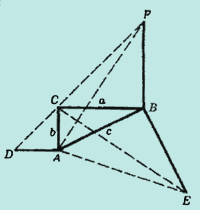
На рисунке изображен треугольник ABC с прямым углом С; отрезок BF перпендикулярен СВ и равен ему, отрезок BE перпендикулярен АВ и равен ему, отрезок AD перпендикулярен АС и равен ему; точки F, С, D принадлежат одной прямой; четырехугольники ADFB и АСВЕ равновелики, так как треугольники ABF и ECB равны; треугольники ADF и АСЕ равновелики; отнимем от обоих равновеликих четырехугольников общий для них треугольник ABC, получим 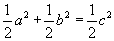. Теорема доказана.