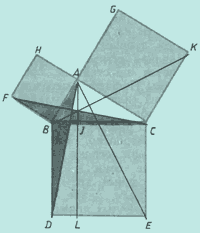
Доказательство Евклида приведено в предложении 47 I книги "Начал". На гипотенузе и катетах прямоугольного треугольника ABC строятся соответствующие квадраты (рис.) и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник JCEL - квадрату ACKG. Тогда сумма квадратов на катетах будет равна квадрату на гипотенузе. В самом деле, затушеванные на рисунке треугольники ABD и BFC равны по двум сторонам и углу между ними: FB=AB, BC=BD и угол FBC равен сумме углов d и ABC, т.е. углу ABD. Но 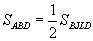так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично, 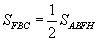(BF - общее основание, АВ - общая высота). Отсюда, учитывая, что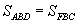, имеем 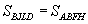Аналогично, используя равенство треугольников ВСК и АСЕ, доказывается, что 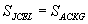. Итак, 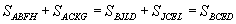, что и требовалось доказать. Доказательство Евклида в сравнении с древнекитайским или древнеиндийским выглядит чрезмерно сложным. По этой причине его нередко называли "ходульным" и "надуманным". Но такое мнение поверхностно. Теорема Пифагора у Евклида является заключительным звеном в цепи предложений I книги "Начал". Для того чтобы логически безупречно построить эту цепь, чтобы каждый шаг доказательства был основан на ранее доказанных предложениях, Евклиду нужен был именно выбранный им путь. Теорема доказана.